数据集:https://www.123pan.com/s/RbfGjv-vOem3.html
提取码:rgzn
一、逻辑回归-预测考试通过

1、导入模块
# 导入模块
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
``
## 2、读取数据
```python
# 读取数据(加载数据,加载后打印首几行确认数据加载成功。)
data = pd.read_csv('../data/examdata.csv')
data.head() # 打印前几行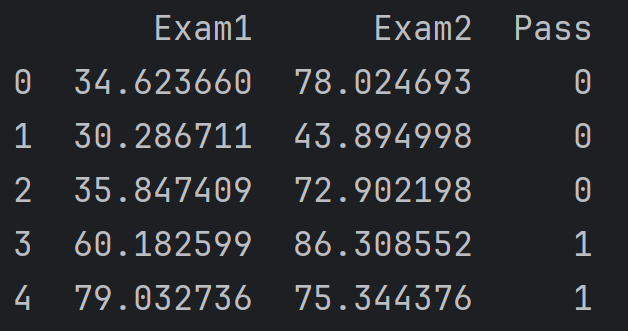
3、可视化数据
# 可视化数据
# 以Exam1为x轴,Exam2为y轴,绘制散点图
fig1 = plt.figure()
plt.scatter(data.loc[:, 'Exam1'], data.loc[:, 'Exam2'])
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.show()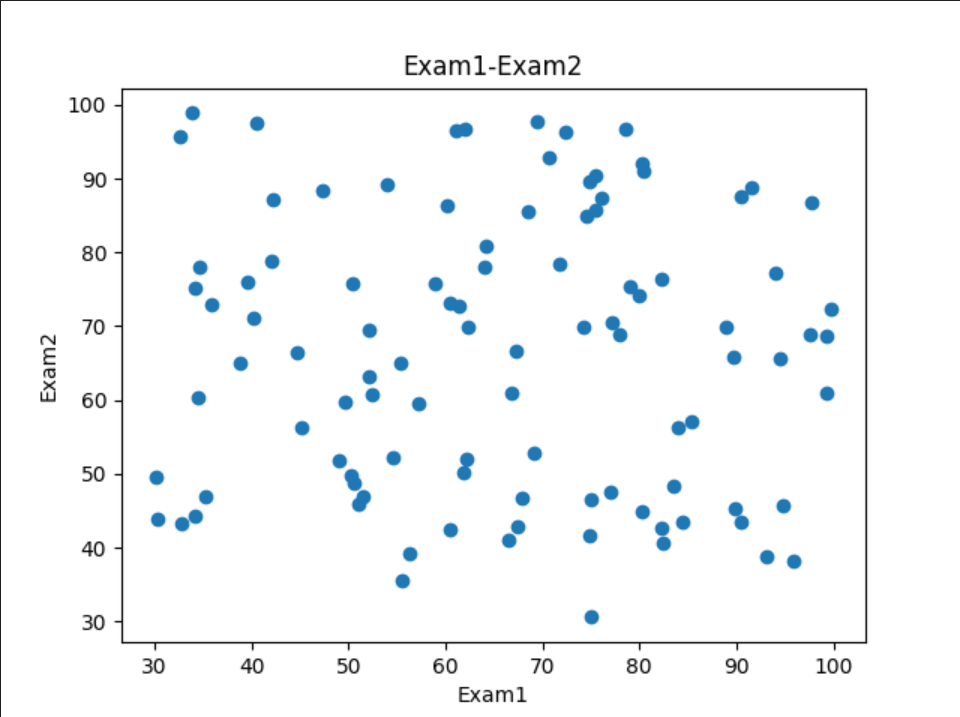
4、添加标签标记
标签标记的作用是,将通过考试的记录标记为True,未通过考试的记录标记为False。方便对通过和未通过的数据进行分离。
# 添加标签标记
mask = data.loc[:, 'Pass'] == 1
# 这个比较操作的结果是一个布尔向量(Boolean Series),其中的值为 True 当对应的 'Pass' 值等于1,否则为 False。
# 这个布尔向量被赋值给变量 mask,通常用于后续的条件过滤或标记。
print(~mask)
# ~是对布尔向量取反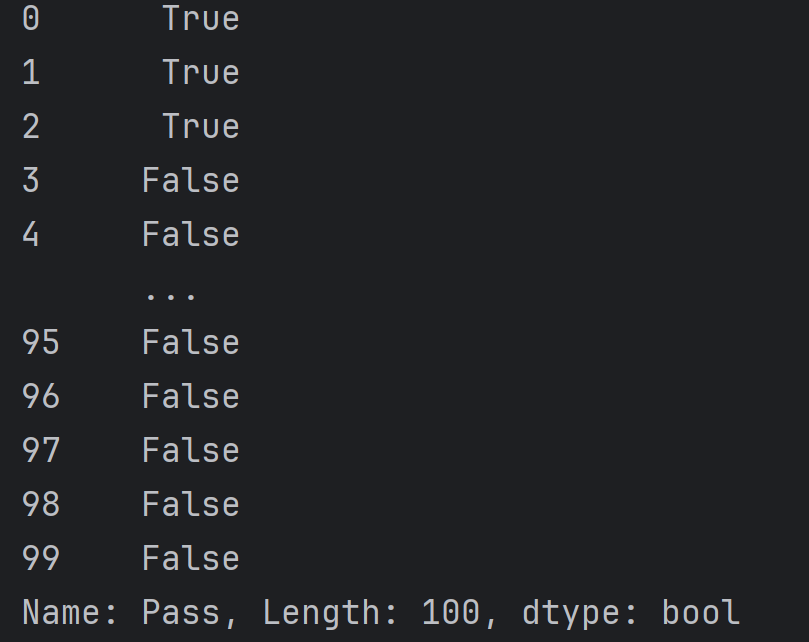
5、将有标记的标签数据可视化
# 将有标记的标签数据可视化
fig2 = plt.figure()
passed = plt.scatter(data.loc[:, 'Exam1'][mask], data.loc[:, 'Exam2'][mask])
# 在新创建的图形上绘制一个散点图,其中x轴是data DataFrame中通过mask筛选出的'Exam1'列的值,y轴是其对应的'Exam2'列的值。
# 这些点代表的是'Pass'列值为1的行,即通过的考试记录。
# 使用passed变量来保存这个散点图对象,以便在图例中显示。
failed = plt.scatter(data.loc[:, 'Exam1'][~mask], data.loc[:, 'Exam2'][~mask])
# 同理failed为未通过考试的散点图
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
# 添加图例,passed和failed是之前散点图的对象,而('passed','failed')是对应图例中的文本标签。
plt.legend((passed, failed), ('passed', 'failed'))
plt.show()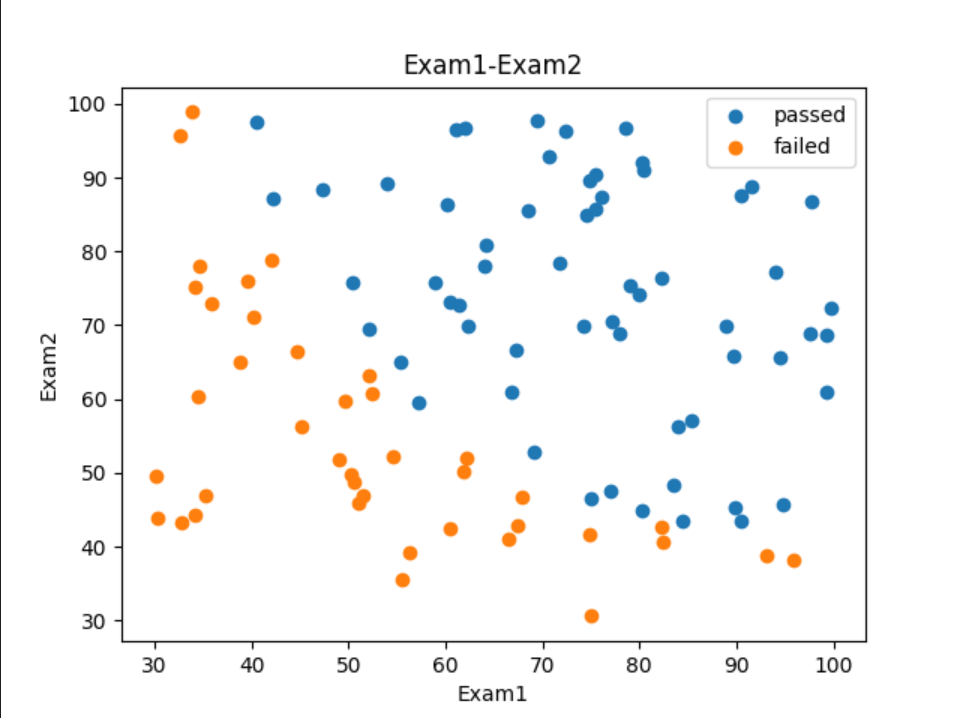
6、定义X、y
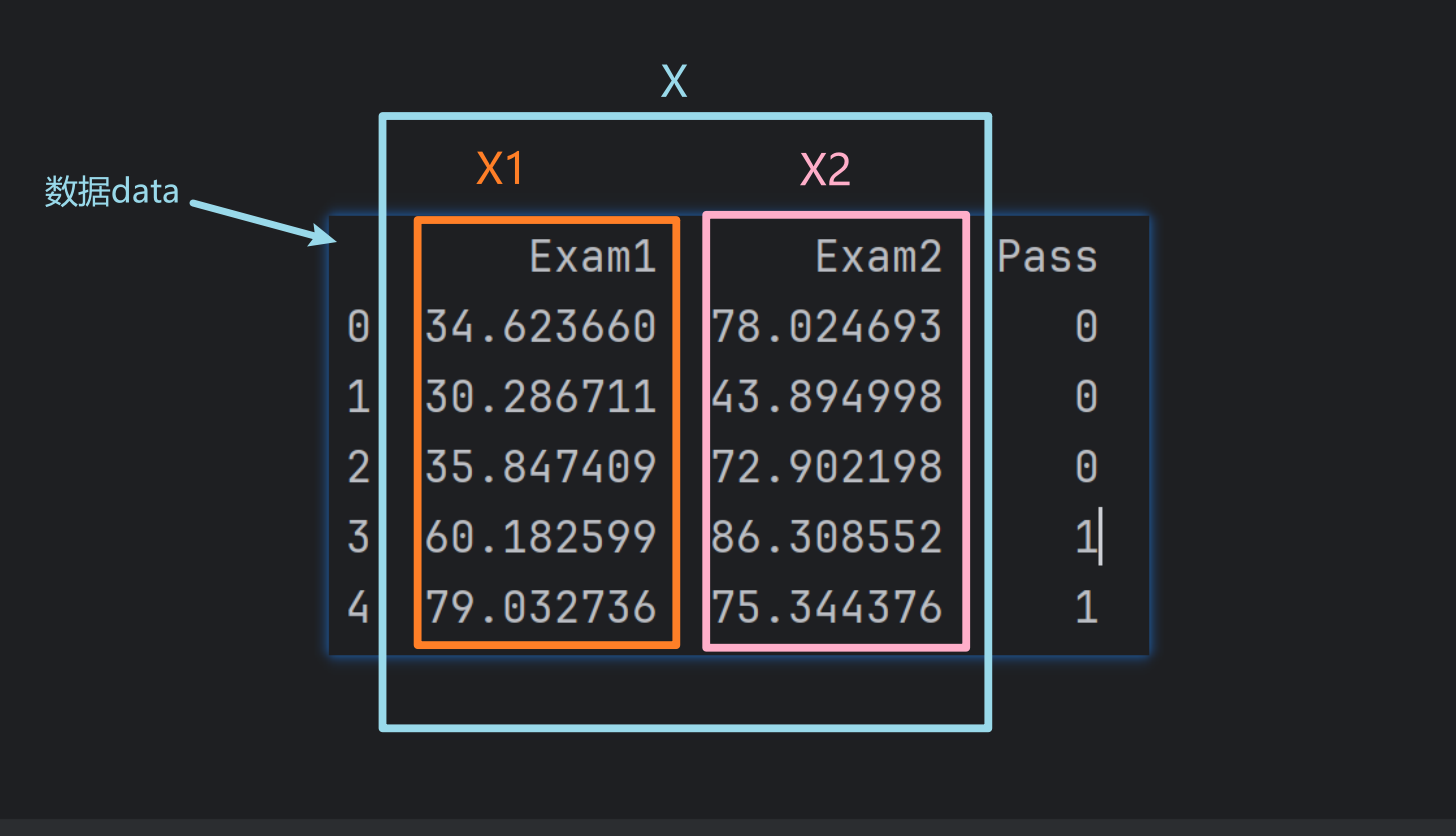
# 定义 X,y
X = data.drop(['Pass'], axis=1)
# drop方法用于移除指定的列。['Pass']表示要移除的列名,axis=1表示移除列,默认是移除行。
# 所以X就是data DataFrame中除了'Pass'列的所有列。
y = data.loc[:, 'Pass'] # y为data DataFrame中'Pass'列
X1 = data.loc[:, 'Exam1'] # X1为data DataFrame中'Exam1'列
X2 = data.loc[:, 'Exam2'] # X2为data DataFrame中'Exam2'列
print(X1.head()) # 打印X1的前几行
print(X.shape, y.shape) # 打印X和y的形状
# X和y的形状:(100, 2) (100,)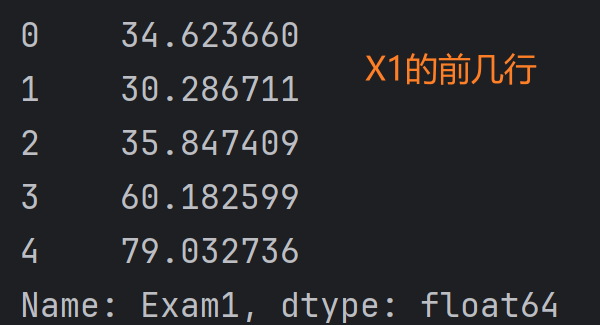
7、建立并训练模型
# 建立并训练模型
LR = LogisticRegression() # 建立逻辑回归模型
LR.fit(X, y) # 训练模型8、预测结果并评估模型
预测结果
# 预测结果
y_predict = LR.predict(X) # 预测结果
print(y_predict)预测结果如下:
[0 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 1 1 0 0 0 0 1
1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 1 1 0 1 1 1
1 1 1 1 0 1 1 1 1 0 1 1 0 1 1 0 1 1 0 1 1 1 1 1 0 1]计算准确率
# 计算准确率
accuracy = accuracy_score(y, y_predict) # 计算准确率
print(accuracy) # 0.89预测exam1=70,exam2=65是否通过
# 预测所给的数据是否通过 exam1=70,exam2=65
y_test = LR.predict([[70, 65]])
print('passed' if y_test == 1 else 'failed') # passed9、计算决策边界
回归模型其实就是一个函数。例如f(x)=theta0+theta1x1+theta2x2
对于这个函数来说,theta0就是它的截距,theta1和theta2就是系数,或者说权重。
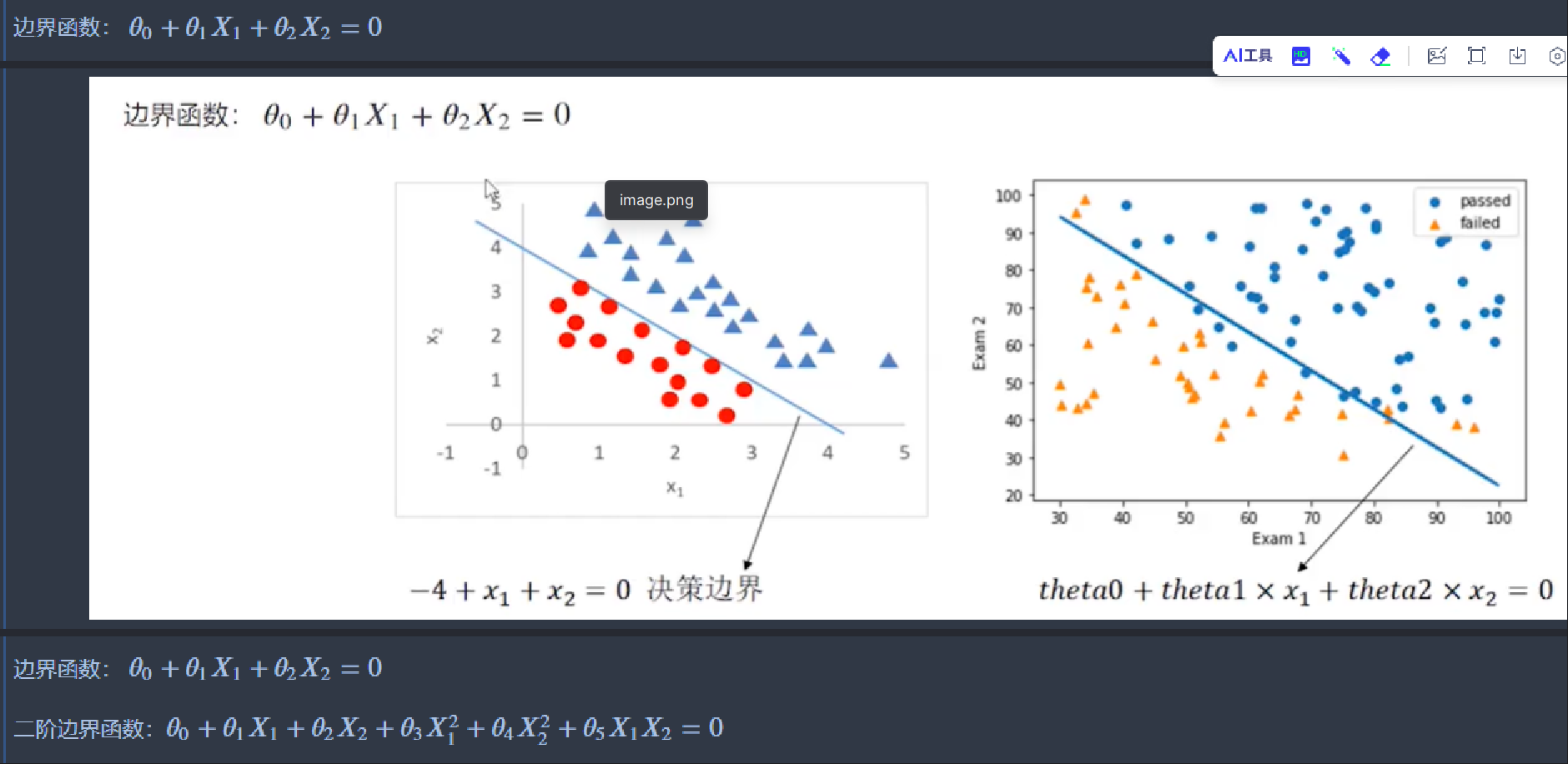
边界函数:theta0+theta1x1+theta2x2=0
对函数变形得x2=-(theta0+theta1*x1)/theta2
回归模型建立好后,theta、theta1、theta2就已经确定了。 边界函数就是关于x1和x2的函数。每给定一个x1,就有一个x2与之对应;把X1作为应变量,就可以计算出X2_new。 X1中的一个值,对应的X2_new的一个值,确定一个点,将这些点连起来,就绘制出边界函数。
获取theta并计算决策边界
系数theta保存在coef_中
# LR2.coef_中存放的是模型的系数,或者说权重。
# print(LR.coef_) # [[0.20535491 0.2005838 ]]# 获取theta0,theta1,theta2
theta0 = LR.intercept_ # 截距项
theta1, theta2 = LR.coef_[0][0], LR.coef_[0][1] # 'Exam1' 和 'Exam2' 的特征权重。
print(theta0, theta1, theta2) # [-25.05219314] 0.205354912177904 0.2005838039546907
# 以X1作为应变量,计算X2_new。
X2_new = -(theta0 + theta1 * X1) / theta2
print(X2_new)X2_new的结果:
0 89.449169
1 93.889277
2 88.196312
3 63.282281
4 43.983773
...
95 39.421346
96 81.629448
97 23.219064
98 68.240049
99 48.341870
Name: Exam1, Length: 100, dtype: float6410、绘制决策边界
# 可视化边界函数
fig3 = plt.figure()
passed = plt.scatter(data.loc[:, 'Exam1'][mask], data.loc[:, 'Exam2'][mask]) # 通过
failed = plt.scatter(data.loc[:, 'Exam1'][~mask], data.loc[:, 'Exam2'][~mask]) # 未通过
plt.plot(X1, X2_new) # 绘制边界函数
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.legend((passed, failed), ('passed', 'failed')) # 添加图例
plt.show()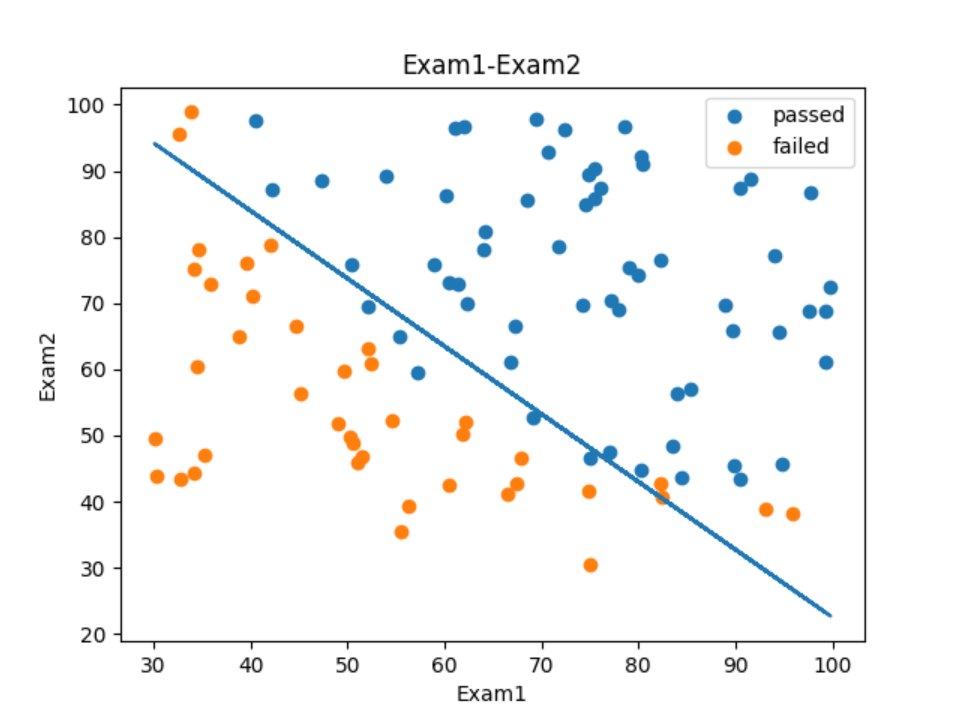
二、逻辑回归-芯片质量检测
1、导入模块
# 导入模块
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
import numpy as np2、加载数据集
#加载数据
import pandas as pd
data = pd.read_csv('../data/chip_test.csv')
print(data)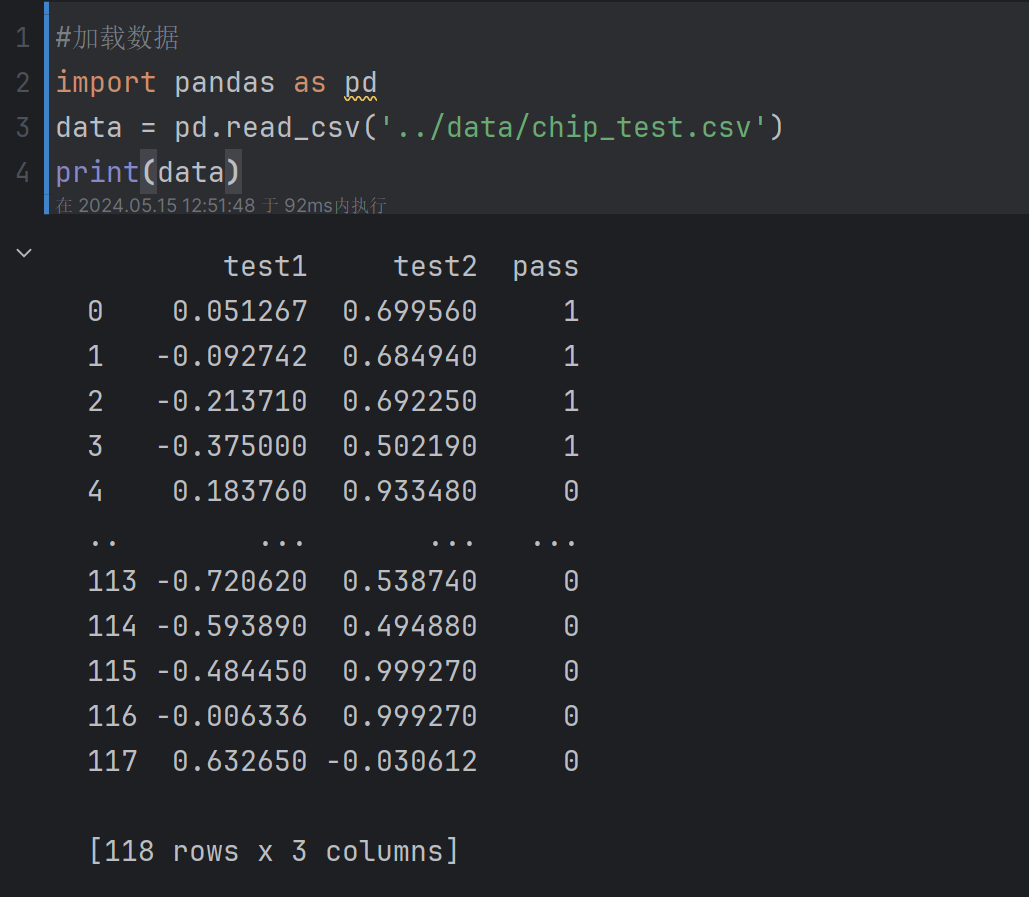
3、添加标记
#添加标记
mask = data.loc[:,'pass']==1
print(mask)
4、可视化有标记的数据
#可视化有标记的数据
import matplotlib.pyplot as plt
fig1 = plt.figure()
passed = plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed = plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()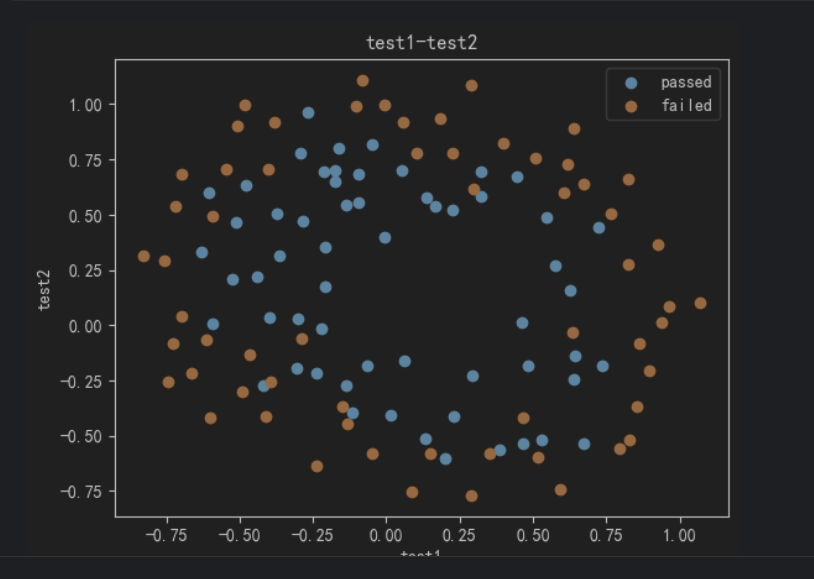
5、定义X、y
#定义 X,y
X = data.drop(['pass'],axis=1) # x为test1和test2两列
y = data.loc[:,'pass'] # y为pass列
X1 = data.loc[:,'test1']
X2 = data.loc[:,'test2']
X1.head()
#create new data
# 增加二次项特征
X1_2 = X1*X1
X2_2 = X2*X2
X1_X2 = X1*X2
X_new = {'X1':X1,'X2':X2,'X1_2':X1_2,'X2_2':X2_2,'X1_X2':X1_X2}
X_new = pd.DataFrame(X_new)
print(X_new)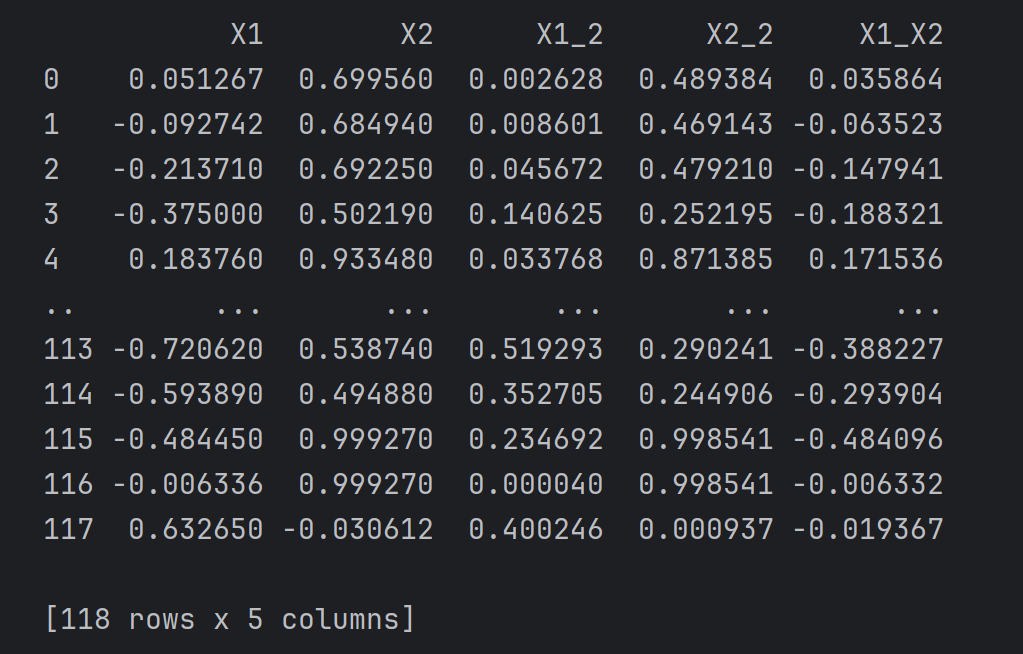
6、建立并训练模型
#建立并训练模型
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
LR.fit(X_new,y)7、评估模型
#评估模型表现
y_predict = LR.predict(X_new) # 使用训练好的模型预测
# 计算准确率
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy) # 0.81355932203389848、初步画决策边界
#初步画决策边界
# 对X1进行排序
X1_new = X1.sort_values()
# 获取theta
theta0 = LR.intercept_
theta1,theta2,theta3,theta4,theta5 = LR.coef_[0][0],LR.coef_[0][1],LR.coef_[0][2],LR.coef_[0][3],LR.coef_[0][4]
# 计算a、b、c
a = theta4
b = theta5*X1_new+theta2
c = theta0+theta1*X1_new+theta3*X1_new*X1_new
# 计算X2_new_boundary
X2_new_boundary = (-b+np.sqrt(b*b-4*a*c))/(2*a)
# 绘制决策边界
fig2 = plt.figure()
passed = plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed = plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_new,X2_new_boundary)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()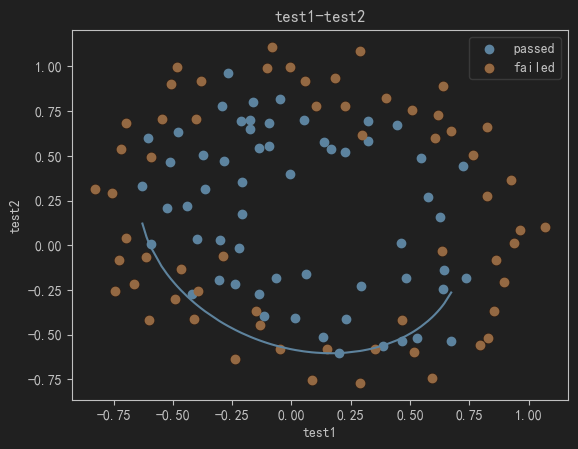
9、画完整的决策边界
plt.show()
#%%
#画完整的决策边界
import numpy as np
d = np.array(b*b-4*a*c) # 判别式deta(拼音)
#d = (-b+np.sqrt(b*b-4*a*c))/(2*a)
X1_new
#print(np.array(d))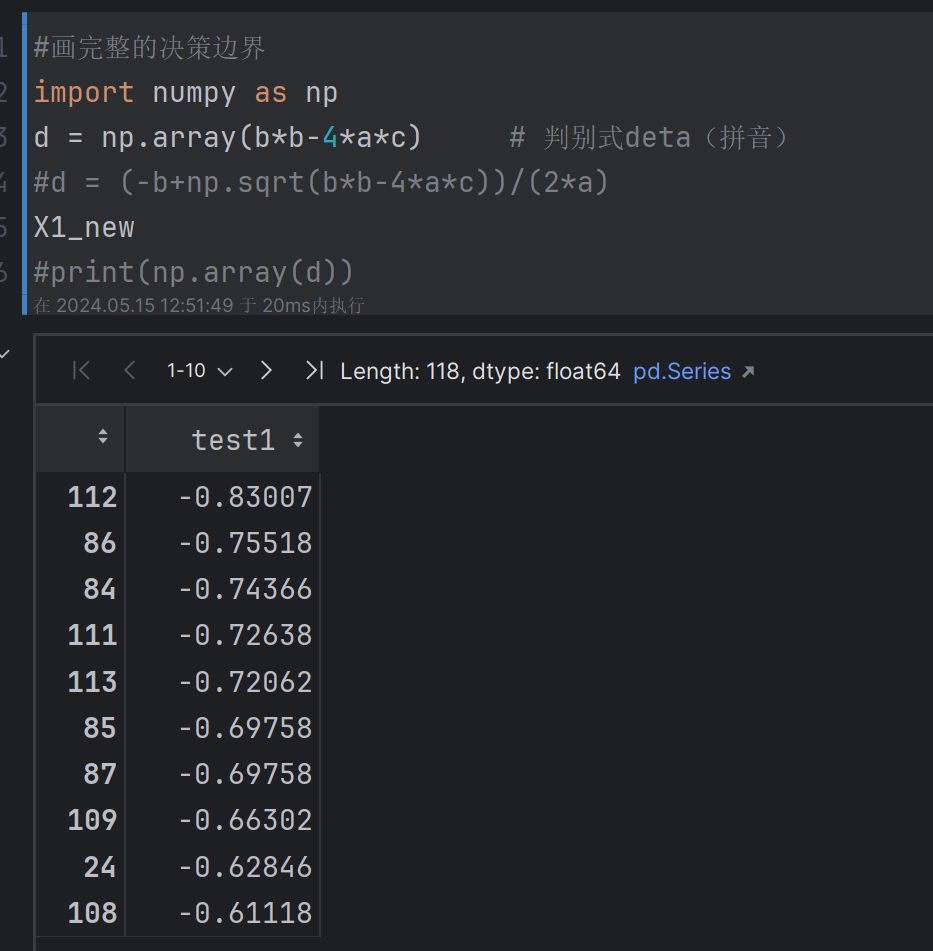
定义f(x)用于计算上边界和下边界
#define f(x)
def f(x):
"""
用于计算上下边界。
函数返回两个值,分别是基于输入x计算出的两个可能的X2边界值。
"""
a = theta4
b = theta5*x+theta2
c = theta0+theta1*x+theta3*x*x
# 方程a*x**2+b*x+c=0的两个根
X2_new_boundary1 = (-b+np.sqrt(b*b-4*a*c))/(2*a) # 上边界
X2_new_boundary2 = (-b-np.sqrt(b*b-4*a*c))/(2*a) # 下边界
return X2_new_boundary1,X2_new_boundary2计算上下边界
# 计算上下边界
# 列表用于存储上下边界的值
X2_new_boundary1 = []
X2_new_boundary2 = []
# 取出x中的每个值,计算出对应的上、下边界
for x in X1_new:
X2_new_boundary1.append(f(x)[0]) # X2_new_boundary1
X2_new_boundary2.append(f(x)[1]) # X2_new_boundary2
print(X2_new_boundary1,X2_new_boundary2)
可视化决策边界
# 可视化决策边界
fig3 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_new,X2_new_boundary1) # 上边界
plt.plot(X1_new,X2_new_boundary2) # 下边界
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()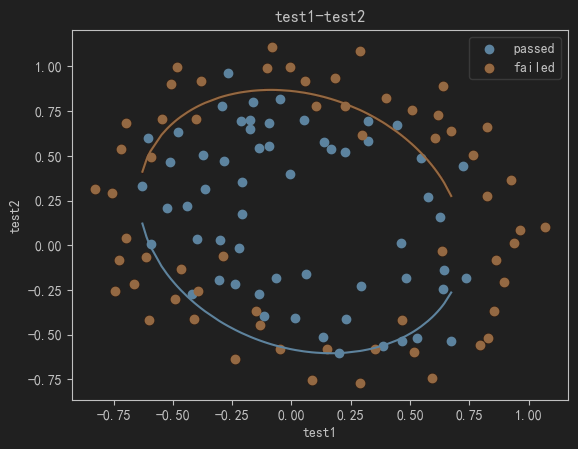
10、在更密集的坐标中画决策边界
#在更密集的坐标中
X1_range = [-0.9 + x/10000 for x in range(0,19000)]
X1_range = np.array(X1_range) # 转换为NumPy数组,计算更高效
X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_range:
X2_new_boundary1.append(f(x)[0])
X2_new_boundary2.append(f(x)[1])可视化
# coding:utf-8
import matplotlib as mlp
mlp.rcParams['font.family'] = 'SimHei' # 设置字体为简体黑体
mlp.rcParams['axes.unicode_minus'] = False # 警用负号
fig4 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
# 上下决策边界,红色
plt.plot(X1_range,X2_new_boundary1,'r')
plt.plot(X1_range,X2_new_boundary2,'r')
plt.title('test1-test2')
plt.xlabel('测试1')
plt.ylabel('测试2')
plt.title('芯片质量预测')
plt.legend((passed,failed),('passed','failed'))
plt.show()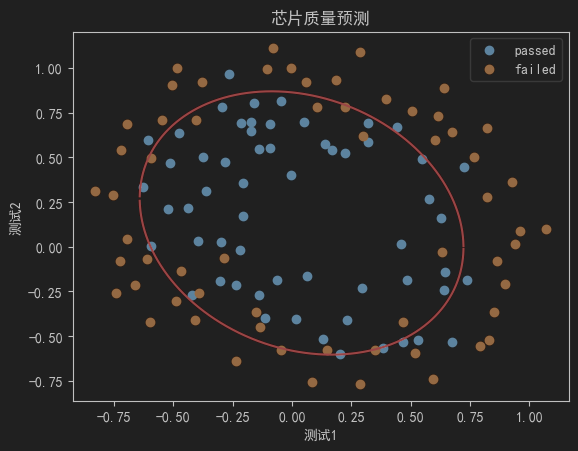
三、逻辑回归-鸢尾花

1、读取鸢尾花数据集
sklearn模块中就有鸢尾花数据集。
# 读取鸢尾花数据集
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[iris.target < 2][:, :2] # 只取前两个特征、前两标签的数据
y = iris.target[iris.target < 2] # 只取0和1标签(前两类)
print(X, y)
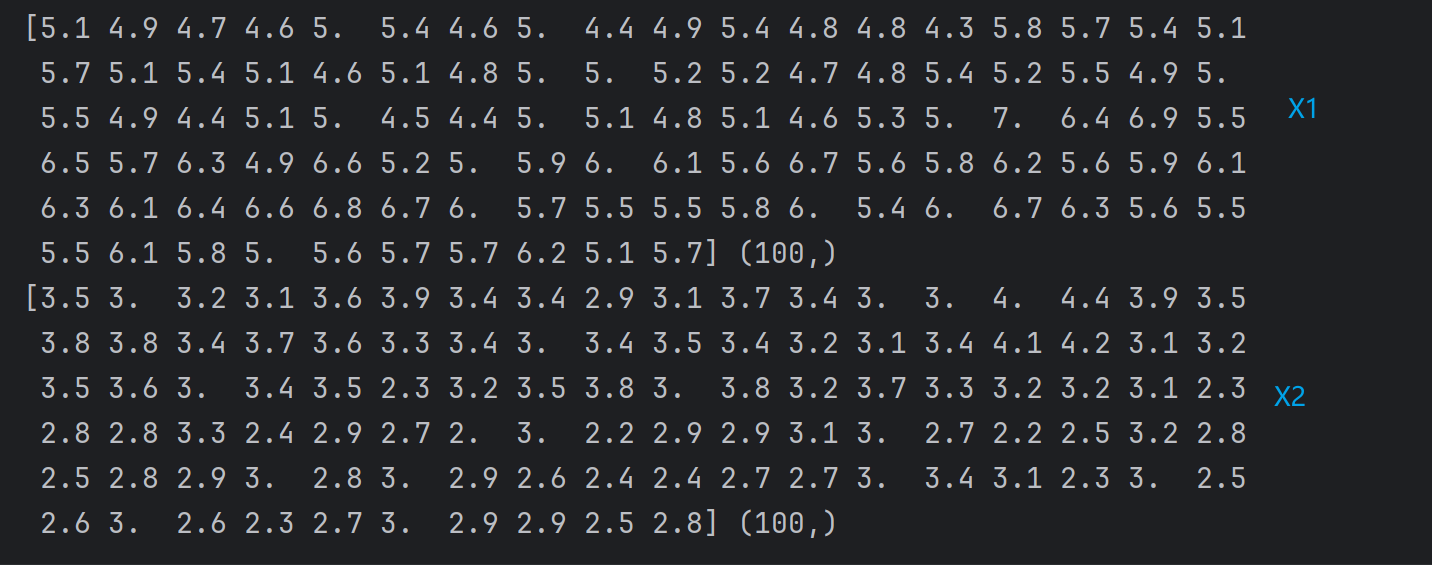
X1 = X[:, 0]
X2 = X[:, 1]
print(X1)
print(X2)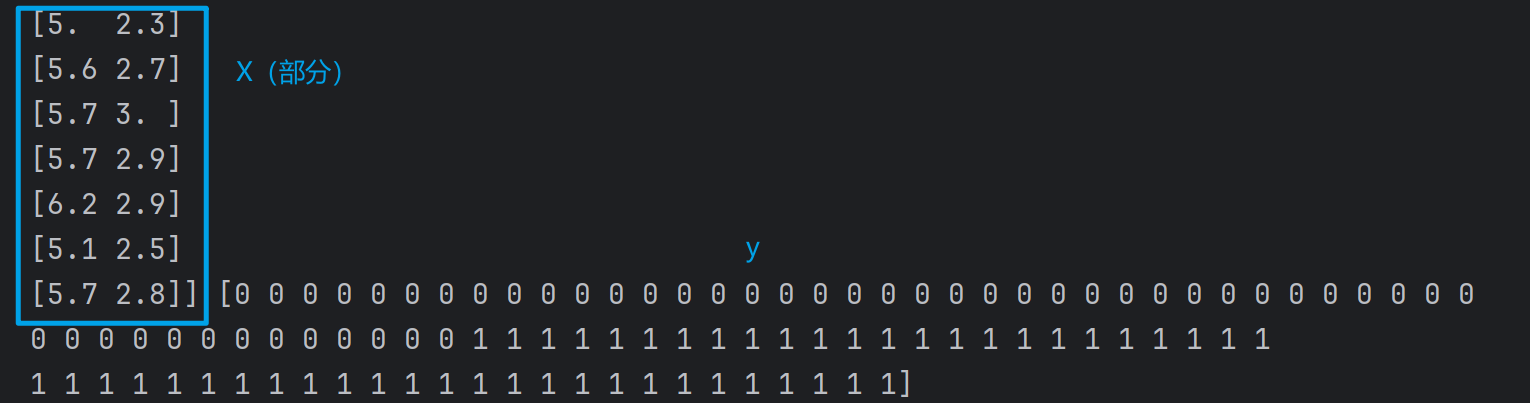
2、可视化数据集
# 可视化
from matplotlib import pyplot as plt
fig1 = plt.figure()
plt.scatter(X1, X2, c=y)
plt.show()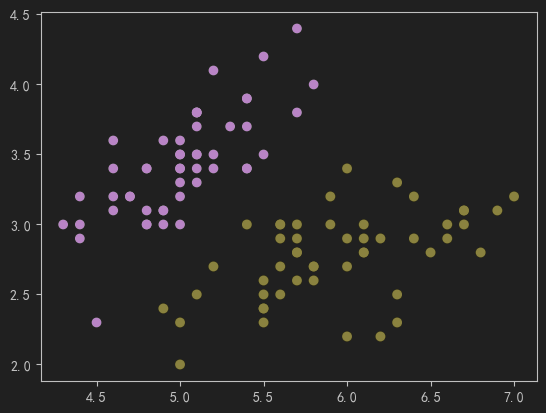
3、建立回归模型并训练
# 建立逻辑回归模型,并训练
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
LR.fit(X,y)4、预测和评估模型
# 预测和评估
y_predict = LR.predict(X)
print(y_predict)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict) # 计算准确率
print(accuracy) # 精确率=1,拟合效果很好
5、计算决策边界
# 计算决策边界
theta0 = LR.intercept_
theta1, theta2 = LR.coef_[0][0], LR.coef_[0][1]
X2_new = (-theta0 - theta1 * X1) / theta2
print(X2_new)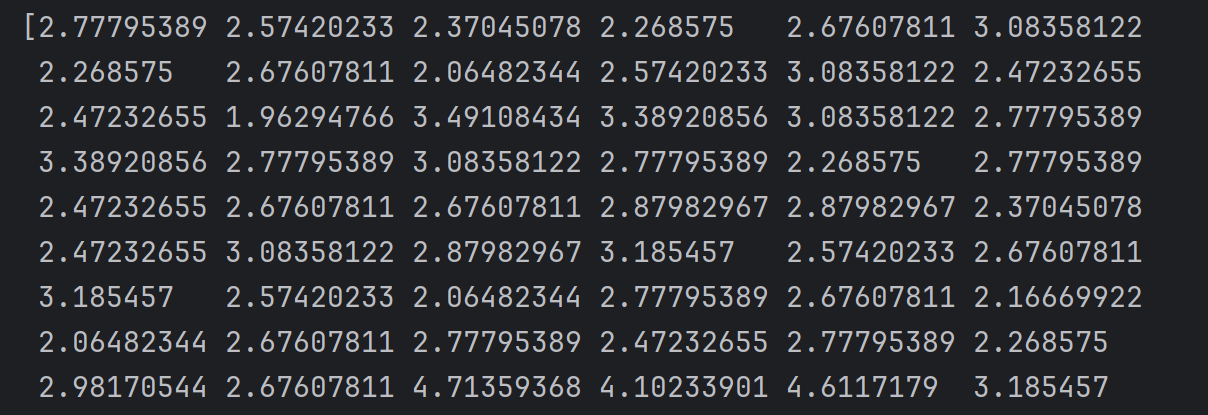
6、可视化决策边界
# 画出决策边界
fig2 = plt.figure()
plt.scatter(X1, X2, c=y)
plt.plot(X1,X2_new)
plt.show()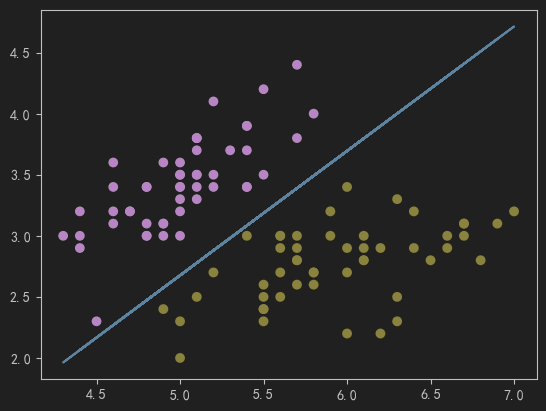
四、逻辑回归知识点



边界函数